Research on Microtonality for HOOLA
I have for many years been deeply fascinated by the concept of microtonality. Microtones may be defined as “intervals which lie between the semi-tones of the 12-note, equal-tempered tuning system” used in Western music [25]. Although this is a somewhat ethnocentric definition (an Arabic musician, for example, might just as well define a microtone as being any interval that lies outside of his or her own scale system) the important thing to acknowledge is that pitch is continuous in nature. Pitch, being a perceptual measure of frequency, should be considered with human limitations in mind – human pitch discrimination is finite, whereas frequency is continuous. Proceeding with this knowledge, one may divide the pitched frequency range in any way that she conceives.
On a semantic note, the term microtone implies frequency intervals which are small, such as those yielded by dividing an octave into 48 equal parts. This is somewhat misleading; a division of an octave into five equal parts, for example, (which also yields notes different from that of the 12-tone, equal-tempered tuning system) qualifies as microtonal just as much.
To Scale or Not to Scale?
In general, when musicians consider microtonality (which they most often do not) they are thinking about musical scales. In light of what has been discussed thus far, it should be clear that there is a near infinite number of scales that one could design. Most scales are created using mathematical formulas used to divide an octave into smaller parts. There are also scales that do not include the interval of an octave at all, based on division of some other interval. Finally, there are microtonal systems that are not concerned with scales whatsoever; for example, a computer algorithm that randomly generates a non-repeating list of numbers to control the frequency of an oscillator is a microtonal system. For the sake of this post, however, I will discuss two of the most common systems used for generating microtonal scales and propose a musical framework in which multiple scales of both types can be combined to create polymicrotonal music. The two systems are called equal temperament and just intonation.
Just Intonation
Equal temperament is much easier to conceive than Just Intonation but is mathematically more complex. Just intonation, on the other hand, is mathematically simple: numeric ratios based on small whole numbers are used to create new notes above a tonic pitch/frequency via multiplication. The quotient of these ratios (which are actually just simple fractions such as 3/2) must lie between 1.0 and 2.0. For example, taking A 440 Hz as a starting point, one can generate a second note by multiplying 440 by 3/2 yielding E 660, which is a harmonically “pure”, or just, perfect fifth. Successive notes can only be generated via the tonic and therefore just scales have a strong sense of tonal center. Although in theory there is no limit to the number of ratios one can include in a just intonation scale, many follow the standard described below.
Harry Partch advocated the use of limits when creating just scales and many microtonalists have continued to follow his model. Limits restrict the number of pitches in a scale based on a specified numeric threshold, a maximum odd number to be allowed in the ratios – only ratios that include odd numbers less than or equal to the chosen number are permitted. Even numbers are inconsequential. Considering a 5-limit scale, for instance, only ratios/fractions which include odd numbers less than or equal to five (in the numerator or denominator) are allowed. The following intervals would therefore be acceptable: 1/1, 6/5, 5/4, 4/3, 3/2, 5/3, 8/5, 2/1. The interval 7/5, on the other hand, would not be allowed in a 5-limit scale, but would fall into the 7-limit. Limits are useful because they determine the possible number of tones in a scale and also influence the amount of dissonance in a scale.
…Just Intonation and Dissonance
According to Partch, whose theories were largely based on the ideas of Helmholtz [31], the dissonance of ratios increases as the odd numbers allowed increases. To some extent it seems that this theory contains truth, that the ear in fact is able to determine ratio complexity. For example, following Partch’s theory, the interval of a tritone (in just intonation traditionally calculated as 45/32 [31]) falls into the 45-limit and is therefore highly dissonant. Contrarily, analyzing the dissonance of this interval using Plomp and Levelt’s conception of consonance, based solely on additive acoustic roughness, yields that the tritone is no more dissonant than a tempered major third [32]. Figure A-1 demonstrates this via use of dissonance curve algorithms created by William Sethares [37].
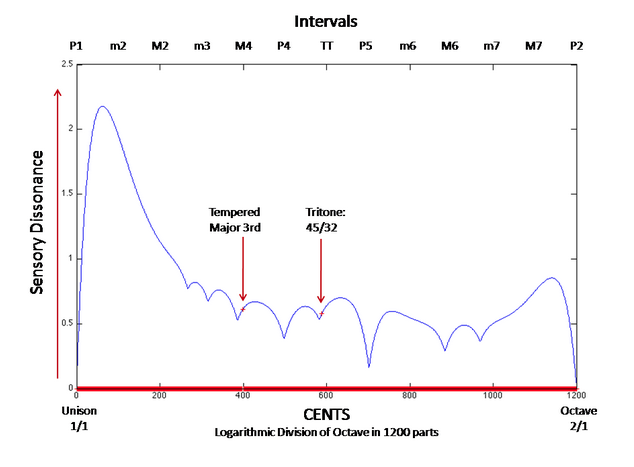
Figure A-1 Plot of a Dissonance Curve
To any musician familiar with harmonic intervals, to postulate that a tritone could in any way be equivalent to a major third seems ludicrous. The fact that Partch’s conception of dissonance seems to capture this is a positive testimony. Partch’s notion of dissonance, however, seemed to ignore timbre altogether and was based solely on numeric ratios. Plomp and Levelt, on the other hand, offered a basis for dissonance that was dynamic, in which the dissonance of an interval is dependent on the chosen timbre [37].
Proponents of just intonation propose that the system offers pure harmonies which are free of acoustic roughness (unpleasant acoustic beating). In general, when compared to equal temperament, primary intervals such as a perfect fifth and major third (calculated in just intonation as 3/2 and 5/4) sound purer due to a lack of unpleasant beating. Considering, however, that just intervals can be used to approximate any pitch if one finds the right (or wrong) ratio, this notion should not be extended too far. The idea, however, that one may determine the relative dissonance of intervals based on the complexity of ratios is an appealing one. For equal tempered scales, which I will discuss next, there is no underlying rule that one may use to pre-determine the quality of individual intervals. Working with equal temperaments, therefore, requires a lot of experimentation.
Equal Temperament
Temperament in general refers to the tempering or shifting of just ratios to create scales which allow for better modulations and transpositions. Equal temperament, specifically, is the division of an octave (or another interval) into a chosen number of equal parts, meaning that each successive note is separated multiplicatively by the same interval. Because we perceive changes in pitch exponentially, we perceive successive tones of equal-tempered scales as being equally spaced. The Western twelve-tone equal temperament tuning system (often abbreviated as 12-TET by microtonalists) is the most common equal-tempered tuning system. Adopted widely by musicians in 17th Century Europe, it was the first system to allow for transposition or modulation into all major and minor keys, corresponding to each of the twelve pitch classes represented on the organ [21]. Musicians had likely desired to have this ability for a long time. J.S. Bach’s work the Well Tempered Clavier, for example, exemplified this interest through its featuring of pieces in all 24 major and minor keys.
The calculation of equal temperaments may be simply achieved using a scientific calculator. For an equal tempered scale of n steps, one simply calculates the nth root of 2, in which 2 corresponds to the interval of an octave. The calculation of twelve tone equal temperament, for instance, can be simply expressed as shown in the equation below. For an equal tempered scale, a single scalar, the result
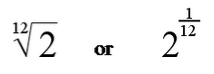
(A.1)
of the equation, is used to generate a scale. Starting on any frequency, one simply multiplies each successive frequency by the scalar until a frequency twice that of the original is obtained, as shown in Figure A-2.

Figure A-2 Equal Temperament Scale Generation
For those interested in experimenting with microtonality, equal temperament offers a convenient starting point because one need only choose one number (the number of notes per octave) to generate an entire scale. As mentioned above, however, the resultant sound of equal tempered scales is unpredictable. The quality of a scale, especially of individual tones within a scale, bears little relation to the chosen number of octave divisions. For example, eleven tone equal-temperament (or 11-TET) sounds nothing like 12-TET and is quite dissonant, which might make it unappealing or difficult for many musicians to work with. On the other hand, 31-TET approximates many consonant harmonic intervals very well and has therefore been adopted by numerous microtonal musicians [43].
Although the quality of equal tempered scales may be largely unpredictable, a convenient tool exists for comparing the location (for instance, halfway between a minor and major 3rd) of an unknown note with that of a familiar one – the use of CENTS (a logarithmic division of the octave into 1200 equally spaced intervals). Taking the twelve tone equal-temperament scale as an example, using the note C as a starting point: C1 = 0 cents, C#1 = 100 cents, G1 = 700 cents, and C2 = 1200 cents. Using this model as a basis of comparison, if we know the cent value of an unfamiliar interval, we can then compare it to an interval that we do know. For a given ratio r one may perform cent conversion using the equation which follows [43].

An Original Approach to Polymicrotonal Composition
For some reason, many microtonal musicians tend to advocate use of one of the microtonal systems described above over the other. Both camps, however, tend to agree upon and advocate making music using anything other than twelve tone equal temperament. I advocate using everything including 12-TET. In retrospect, most composers first turned to experimenting with microtonality in order to expand the range of musical possibilities; why do they limit themselves now? Specifically, why do they adhere to a particular system?
The answer is likely a practical one. Traditionally, composers of microtonal music have faced challenges in having their music realized because performers have been untrained and uninterested in microtonality and because few instruments existed which could play microtones. By adhering to a particular system, or even a single scale, eventually a composer might have found outlets for his or her music.
Recently, through use of computers and other electronic musical equipment it has become possible to program any combination of microtonal scales that one can imagine with little effort. Nevertheless, to have such music performed is still a difficult task due to an enduring lack of microtonally conceived instruments and resistance from performers. Putting these issues aside, if one can imagine a polymicrotonal musical system, he or she would likely hope for it to follow some overarching logic, to be both mathematically and theoretically sound, and to be easily perceivable (meaning that a listener can hear what’s going on). Ultimately, one might also hope that the music could actually be performed. The system I am about to describe meets all of these requirements.
While composing music for HOOLA 1.0 I stumbled upon the concept which I will discuss now. I was considering melodic contour as a basis for melodic composition, without consideration of specific scales. I was thinking about ways in which a generalized contour could be applied to numerous scales, modes, or tuning systems. Consider the following example: take a traditional melody like that of “Happy Birthday” and play it using a minor mode instead of the major scale. Although the individual intervals will be distorted, the overall identity of the tune remains intact – the melody is still recognizable. Now, imagine taking this taking this example to the extreme by applying it to your own complex melodic inventions.
To realize the concept of a generalized melodic contour, I decided initially to experiment with rising and falling glissandi – in practice, these were sinusoidal chirps produced in Matlab and later Max/MSP. I created a simple system using sidechain compression in which the sinusoidal chirps were only allowed to sound when excited by a secondary rhythmic signal. The first glissando that I programmed was a linear frequency chirp which repeatedly ascended and descended over the span of an octave within a prescribed time frame.
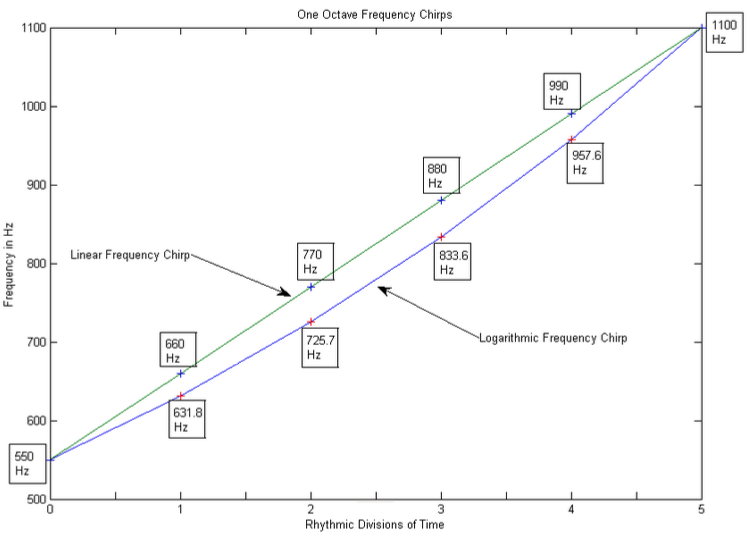
Figure A-3 Scales Generated Via Sinusoidal Chirp Division
To excite the signal, I used short rhythmic bursts timed to divide the octave-glissando into equal parts of various numbers, emitting what sounded like unusual musical scales. What I noticed immediately, based on my experience working as a microtonal composer, was that the scales I was hearing sounded like just intonation scales. I verified what frequencies were being sounded and realized that my theory was correct. Based on this finding, my next theory was that following the process described above using instead a base 2 logarithmic sinusoidal chirp would produce equal tempered scales. This also proved to be true. Figure A-3 demonstrates the process and illustrates the scales created by dividing linear and logarithmic octave glissandi into five equal parts.
What was most satisfying, however, was the discovery that playing scales of the same number (for instance those created by dividing a linear or a logarithmic glissando into eight equal parts) in conjunction with one another sounded very natural, as if they were related in some inherent way. Using the method I have described I created scales of five, six, seven, eight, and nine notes per octave based on division of both the linear octave and logarithmic octave; this yielded ten scales in total and seventy distinct pitches. Importantly, in practice I was able to create a system in which music using these scales could be easily performed using five hula hoop instruments. Playing such scales fortunately does not require an instrument consisting of seventy buttons, but can be easily played using individual instruments with as few as five, six, seven, eight, or nine sensors.
The actual just intonation and equal temperament scales produced using the method described above follow two separate but similarly simple logics. The logarithmic octave divisions simply yield equal tempered scales; dividing the octave into eight parts for instance will yield an 8-tone equal temperament scale. Linear octave divisions on the other hand produce just intervals, simple ratios in which a multiple of the divider will be the numerator; dividing the octave into eight parts will yield the following intervals: 1/1, 16/15, 8/7, 16/13, 4/3, 16/11, 8/5, and 16/9.
Acknowledging my own implication that microtonality will likely never become popular on any grand scale, I do not wish to overemphasize the importance of the system I have described. Nevertheless, for those already working microtonally, or those interested in starting, the system described here provides a theoretically and perceptually sound basis for microtonal music exploration. It offers a user the flexibility to create a scale, or scales, of as many notes as he wishes to experiment with at a given time. For a novice microtonal composer, uncomfortable composing a piece for fifty notes per octave, this system allows her a means of gradually expanding the available palette of pitches.